Following up on my previous post, one of the most interesting aspects of Gaus’s work on ideal/non-ideal theories of justice is that he suggests a formal model in which we can think about the issue. Gaus is quite explicit in stressing the advantages of formal modelling in the introduction to his book. In particular, the outlines of the model Gaus develops are clearly inspired by the idea of fitness landscapes from evolutionary biology; and the contrast between his ideal and non-ideal theories of justice looks a lot like the search for an efficient search algorithm on such landscapes.
So Gaus liberally exploits models from the sciences to think about the pursuit of justice; and this strikes me as a valuable, interesting strategy. But while Gaus sketches a formal model, and spends lots of time on developing various aspects of it, it remains seriously incomplete. In particular, Gaus never suggests—or comes close to suggesting—a way how we can translate the contrast between ideal and non-ideal theories into concrete algorithms within the context of a specified mathematical model. Nor does Gaus spend much time at all on evaluating the success of actual search algorithms, or surveying the literature on the success of such algorithms.
This is a curious omission. In fact, in the crucial part of his book, when Gaus levels his ultimate charge against “ideal” theories of justice, he falls back on mostly non-technical arguments that I found rather unconvincing (though this is a story for another day). Here I’ll make some preliminary observations about how Gaus’s hints could be translated into an actual model, and which challenges we face along the way.
The Basic Model
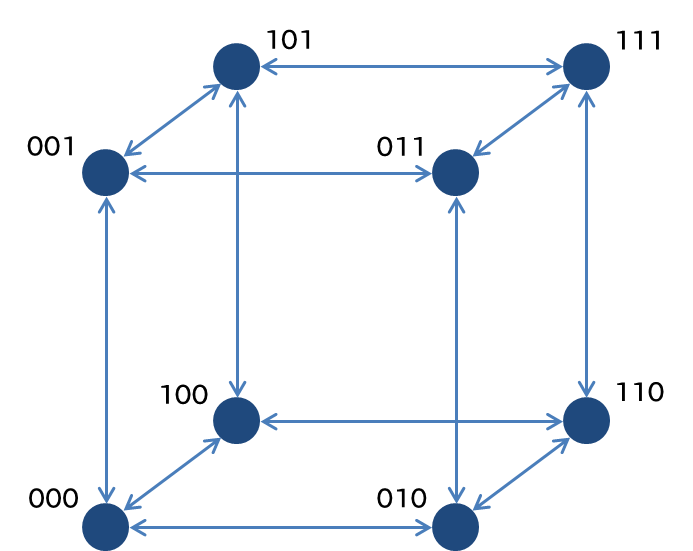
Most of the basic model assumptions of a more complete model can be gleaned easily from Gaus. The task he wishes to model is the pursuit of justice by a society, which we can simplifyingly think of as a homogenous agent. We assume that there are different ways how our society could be. We assign a justice score S to each type of society. We model a society as a set of binary characteristics—e.g., whether it has features A, and whether it has feature B, and so on. More technically, we represents societies as strings of length n—e.g., 10110 for n=5. The distance between two strings is measured by the number of bits in which they differ—e.g., the distance between 10110 and 11010 is 2, as they have two differing bits.
The various possible strings form a connected landscape such that there is a bidirectional path between every two strings with distance 1. That is, if our current society has characteristics 01001, then we face the choice of changing our society to 11001, 00001, 01101, 01011, or 01000 (or keep it unchanged). A connected landscape for n=3, for example, would look as follows.
The advantage of the NK model, as Gaus highlights, is that it provides us with a mathematically elegant way to model the “ruggedness” of a landscape through a single parameter, which is represented by k. Roughly, the higher we set k, the more chaotic our landscape will be: it will have more local, non-global optima. I’ll omit the technical detail of how the value of particular strings is determined in an NK model—these details can be obtained in many places.
The Search Problem
The problem posed by Gaus’s model is decently clear. Agents—i.e., societies—aim to maximize S, but they only see their immediate surroundings (strings with one differing bit). So they must decide on some type of algorithm to work their way through the landscape. We allow agents to move across the landscape one step at a time, and iterate the simulation over some number of steps.
Two dangers await our searchers. On the one hand, they must avoid getting stuck on inferior local optima; at the same time, they must avoid drudging for too long through inferior parts of the landscape in search of better optima. We can think of the performance of an algorithm as the average score it achieves over time, but we could also assess it by other measurements (e.g., the probability that an agent following some algorithm finds the global optimum).
Problems and Challenges
This model has outlines that are decently clear, and which can be modelled without serious trouble. (It took me a couple of hours of very amateurish programming to get a basic model up and running.) The main task which remains is to formulate the competing algorithms and measure their performance for different parameters of the model.
It’s at this point that we encounter the first serious unclarities. I would interpret Gaus as considering two different types of search algorithms. Ideal-type search algorithms try to find the global optimum in the landscape. Putting it vaguely, orientation towards the (perceived) global optimum plays a significant role in such algorithms. By contrast, non-ideal-type search algorithms pay no attention to the perceived global optimum. By comparing these two types of algorithms, Gaus thus hopes to shed light on the ideal/non-ideal distinction.
Let’s think about formulating the relevant algorithms first. Different types of search algorithms fit either description. A very simple “non-ideal” algorithm would be, for example,
Simple Climbing. At any step, choose the neighbouring string with the highest score.
A more sophisticated climbing algorithm would explore some of surrounding landscape first to avoid getting stuck on the first local optimum which offers itself; the literature on search algorithms suggest that such algorithms (“simulated annealing”, “tabu search”) often outperform simple climbing algorithms. It would be interesting to think about the equivalents of these algorithms in political philosophy (Gaus doesn’t), but let’s put the issue aside.
What about an “ideal” search algorithm? Here’s a simple formulation,
Simple Distance Reducing. At any step, choose one of the neighbouring strings with the shortest distance to the global maximum.
Some quick reflection reveals, however, that this isn’t really a search algorithm. If the global maximum is already known, then Simple Distance Reducing is almost trivially the best way to orient yourself in the landscape. It would be foolish to follow any algorithm other than this. But then, of course, if the global optimum is known we’re not really facing a search problem in the first place. So we would need to give some other formulation of an “ideal” algorithm—for example,
Continuous Searching. Search the landscape—in a random or some structured pattern—until you find the global maximum.
This formulation does not rely on the assumption that we know the global optimum. But in which sense, then, is it still an instance of “ideal” theorising? Is any algorithm which involves searching the landscape to some degree a representative of an “ideal” approach to justice? Either way, there are other significant unclarities—how does this algorithm explore the landscape? how does it find out that it has reached the global maximum, short of exploring the full landscape? We can anticipate that some simple versions of this algorithm will perform very badly—greatly inferior to a Simple Climbing algorithm, for example.
I’m sceptical that these problems can be resolved in an easy way. At least, we would need much more specification of the comparisons we’re supposed to make. I also suspect that many of the most successful algorithms for searching through NK landscapes are not easily classified as “ideal” or “non-ideal” types of algorithms (or “utopian” versus “non-utopian”, or whatever contrast you prefer), or do not track any idea which has a useful analogue in political philosophy. In any case, we need much more substance to the model to decide the issue either way.
Other Shortcomings
Just to nag a bit more, let me highlight some other issues. A first question is why we should use the NK model, rather than some other, simpler model for a landscape. Standard agent-based modelling uses torus-shaped 2D landscapes, for example, which can be easily programmed in a modelling language like Netlogo. While NK-models are mathematically very elegant, they are much harder to visualise and intuitively understand; in general, it’s not clear what we gain from thinking about n-dimensional landscapes. The recurring metaphor of “climbing a mountain” that Gaus adopts from Sen and other philosophers also suggests a much simpler, two-dimensional model.
The deeper question is whether the choice between different algorithms really has much to do with the ideal/non-ideal distinction at all (though to be clear, this is based on my reading of how a Gaus-based model would work). Rather, the dimension across which we can distinguish the various algorithms has more to do with how greedy or exploratory they are. That has more to do with utopian practice rather than ideal methodology. This doesn’t make the model uninteresting, though it might be slightly misleading to label it as an ideal/non-ideal issue.
Epistemic Limitations
One crucial modelling assumption I’ve left untouched so far is the idea that agents are near-sighted—that is, Gaus assumes that we’re decently reliable in estimating the justice of societies similar to ours, but very unreliable in doing so for societies which are very unlike ours. This would suggest significant modifications to our basic model. First, we would need to give agents some type of perception function ranging over the strings in our landscape, where perception is some function of the real value of those strings, the agent’s distance to them, and some perturbing factor which increases with distance.
This raises various questions once we try to build this into a concrete model. We now imagine agents which can see much farther than their immediate neighbours. This suggests a much more complicated class of agents which plot their path several steps in advance. A utopian algorithm would then presumably be one which looked to peaks perceived far away; non-utopian algorithms would only take their immediate, reliably perceived neighbourhood into account.
The immediate point here is that the different types of algorithms we must consider as potential solutions for our search problem proliferate exponentially. I have already criticised that the precise formulations of algorithms in the simple model are unclear; in the expanded model under consideration now, it’s even less clear which algorithms we should classify as “ideal” or “non-ideal”. In particular, what about algorithms which are hybrids or “medium-sighted” approaches—that is, algorithms which sometimes aim for uncertain, far-away peaks, but at other times are satisfied with a local optimum? I also suspect that non-dogmatic algorithms of this kind have high chances of success.
(Other practical problems abound. Agents might be caught in vicious cycles—e.g., where string A looks best from viewpoint B, and B looks best from A. So probably we want to give agents some rudimentary memory about the points they’ve already visited. But that significantly increases the complexity of the model and the relevant algorithms again.)
Note that the simple model I started from—where agents only know the value of their immediate neighbours—already has an assumption of limited knowledge built into it, and a particularly stark one at that. So we might as well explore the possibilities of this model first, before we move on to the more complicated model here suggested.
The Promise of Modelling
Either way, to test which type of algorithms are superior in a formal model we would need significantly more pointers as to how to build such a model. In the process, we would need to solve lots of practical model-building problems—both more theoretical (which assumptions are important to model, and where should we simplify?) and practical (which types of algorithms and landscapes are easy to understand and program?).
But assume we have resolved the issues, and test our model. What would the results be? Most immediately, that some complex algorithm of this type is expectably superior to complex algorithms of that type, at least under certain parameters of our model. (Change in parameters, such as the ruggedness of the landscape and how reliably sighted agents are, will have a significant impact, so this will be a heavily conditional result.) To make those results philosophically fruitful, we would then need to re-translate those results into some claim in political philosophy. This again is fraught with difficulties and obstacles, just as interpreting the implications of any highly abstract model-building for the real world is difficult and contentious.
Still, such work could be a valuable contribution to various debates in political philosophy. Building an explicit model forces you to think through various assumptions in a systematic way, and it can reveal various factors that you’re unlikely to think about while doing “pure” normative theorising. But I suspect that the intellectual labour we have to put into getting to such a full-fledged model of this kind stands in no proportion to the gains of such a model, at least as far as philosophical insight is concerned.
It’s only for the better then, perhaps, that Gaus didn’t flesh out a fully developed model in his book. The most charitable reading is that Gaus uses various formal ideas from various scientific models for the purpose I’ve just outlined—as a source of inspiration for political philosophy, and as a way to sketch out some ideas with greater clarity and coherence. This is a much less systematic way to appropriate more technical ideas—it doesn’t amount to building a model—but needn’t be less valuable for that reason.